目次
以前 TensorFlow Playground というニューラルネットワークデモツールを使用したので、使い方などまとめてみました。
TensorFlow Playgroundとは?
そもそも TensorFlow は、Google が開発したオープンソースの機械学習フレームワークで、ニューラルネットワークを含む様々な機械学習モデルの構築、トレーニング、デプロイを行うための豊富なツールやライブラリを提供しています。
そして TensorFlow Playground は、TensorFlow のインタラクティブなデモおよび学習環境です。Webベースのツールで、ブラウザ上で機械学習モデルを構築し、実験することができます。
TensorFlow Playground では、ニューラルネットワークの学習に関するさまざまな概念やハイパーパラメータの影響を直感的に理解することができます。ネットワークの構造や活性化関数、学習率などのパラメータを調整しながら、リアルタイムで学習の進行や予測結果を視覚化することができます。
TensorFlow Playground は、初心者にとっては機械学習の基礎を学ぶための有用なツールであり、経験豊富なユーザーにとってはアイデアの検証やプロトタイピングのための便利な環境です。もちろん無料です。
ニューラルネットワークの基礎
ニューラルネットワークは、人間の脳の仕組みに着想を得た機械学習の手法です。
多層のニューロン(ノード)から構成され、入力データから特徴を学習し、予測や分類を行います。
基本的な構造:
- 入力層: データをネットワークに取り込む部分です。例えば、画像認識ではピクセルデータが入力されます。
- 隠れ層(中間層): 入力データを処理する中間の層です。隠れ層の数やニューロンの数はネットワークの複雑さに応じて変わります。
- 出力層: 処理結果を出力する部分です。例えば、画像が犬か猫かを分類する場合、出力層が「犬」か「猫」のどちらかを示します。
ニューラルネットワークは、活性化関数や重みを調整することで、学習や予測の精度を向上させることができます。
TensorFlow Playground の構成
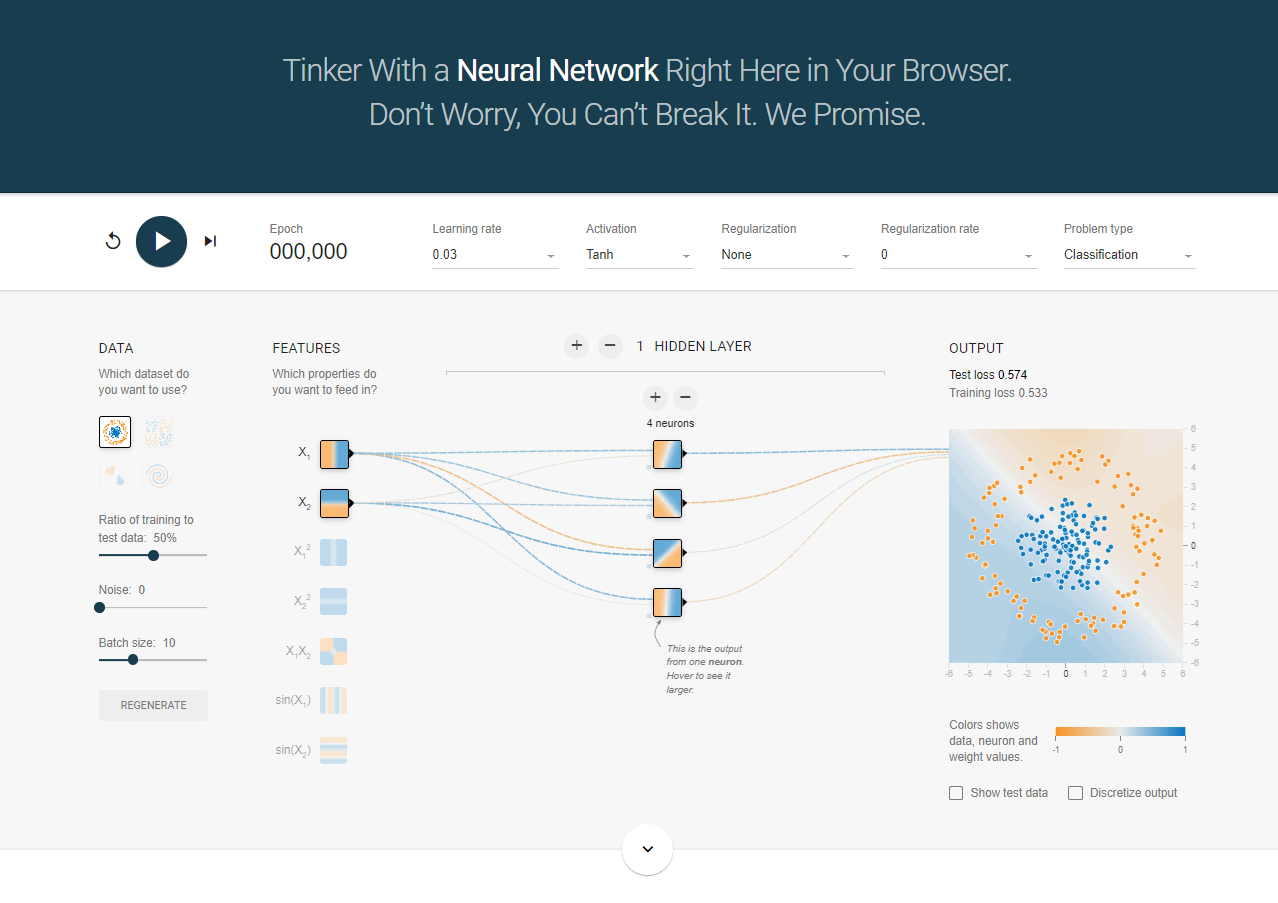
TensorFlow Playgroundの使い方は非常にシンプルで、ページにアクセスするとすぐ使うことができます。リンクはこちら。開くと下の画面が表示されます。

下にスクロールすると、ニューラルネットワークに関する説明や、TensorFlow Playground に関する簡単な説明などが記載されています。

ここでは一旦画面上のそれぞれの意味を説明します。
- 画面上部

- Epoch(エポック)
- エポックは、ニューラルネットワークの学習におけるステップ数を表します。1つのエポックは、訓練データセット内のすべてのサンプルをネットワークに与えて学習を完了するまでのステップです。エポック数はネットワークが訓練データを何回学習するかを示し、モデルの学習の進行状況や収束性を制御するための重要なハイパーパラメータです。適切なエポック数を選ぶことで、モデルは訓練データに適切な程度で適合し、未知のデータに対しても良好な予測性能を持つことが期待されます。また過学習を避けるためには、エポック数を適切に調整する必要があります。
- ここではエポック数の設定はできず、左隣の実行ボタンを押してからカウントされていくのみとなっています。

- Learning rate(学習率)
- 学習率は、ニューラルネットワークの学習において、パラメータの更新量を制御するためのハイパーパラメータです。学習アルゴリズム(一般的には勾配降下法)に基づいて、重みやバイアスを調整する際に使用されます。学習率が小さすぎると収束に時間がかかりますが、大きすぎると収束しない可能性があります。適切な学習率を選ぶことは、モデルの収束速度や性能に大きな影響を与えます。
- ここでは 0.00001 ~ 10 までの 11 分割の数値を選択できます。

- Activation(活性化関数)
- 活性化関数は、ニューラルネットワークの各層における出力値を指します。入力データに対して重みとバイアスの線形結合を行った後、活性化関数によって変換されます。活性化関数は非線形な関数であり、ネットワークが非線形な関数を表現する能力を持つことを可能にします。
- ここでは ReLU、Tanh、Sigmoid、Linearが選択できます。

- ReLU
- ReLU関数は、入力が0以下の場合に0を出力し、0より大きい場合には入力値をそのまま出力します。ReLU関数は以下のような数式で表されます:
- ここで、x は入力値であり、f(x) は出力値です。グラフで表すと以下になります。
- ReLU関数は非線形かつ単純な形状を持ち、計算が効率的であるためニューラルネットワークで広く使用されています。
- Tanh
- Tanh関数は、入力を -1 から 1 の範囲に変換します。Tanh関数は以下のような数式で表されます:
- ここで、x は入力値であり、f(x) は出力値です。グラフで表すと以下になります。
- Tanh関数はシグモイド関数の拡張版と見なすことができ、S字形の曲線を描きます。入力が大きい場合は 1 に近づき、小さい場合は -1 に近づきます。
- Sigmoid
- シグモイド関数は、入力値を 0 から 1 の範囲に変換します。シグモイド関数は以下のような数式で表されます:
- ここで、x は入力値であり、f(x) は出力値です。グラフで表すと以下になります。
- シグモイド関数はS字形の曲線を描き、入力が大きいほど1に近づき、小さいほど0に近づきます。過去には主流の活性化関数でしたが、最近では一部の問題での利用が減っています。
- Linear
- 線形関数(恒等関数)は、入力値をそのまま出力します。線形関数は以下のような数式で表されます:
- ここで、x は入力値であり、f(x) は出力値です。グラフで表すと以下になります。
- 線形関数は非線形変換を行わず、単純に入力値を伝達するだけです。このため、非線形な問題には適していませんが、回帰タスクなどで使用される場合があります。
- Regularization(正則化)
- 正則化は、過学習(モデルが訓練データに対して過度に適合し、未知のデータに対する予測性能が低下する現象)を緩和するための手法です。正則化は、モデルの複雑さにペナルティを課すことによって実現されます。よく使用される正則化手法には、L1正則化、L2正則化などがあります。これらの手法は、モデルの損失関数に正則化項を追加し、重みを制約することで、過学習を抑制します。
- ここではL1正則化かL2正則化を選択できます。

- L1
- L1正則化は、重みの絶対値の合計に比例したペナルティを課す手法です。L1正則化によって、いくつかの重みが厳密に 0 になる傾向があります。これにより、特徴の選択やスパース性(スパースな解)を促進する効果があります。L1正則化の式は以下のように表されます:
- ここで、λ は正則化率を制御するハイパーパラメータであり、w は重みの値です。
- L2
- L2正則化は、重みの二乗和に比例したペナルティを課す手法です。L2正則化によって、重みは 0 に厳密にならないものの、小さな値に抑制されます。L2正則化は、モデルのパラメータを滑らかな値に制約する効果があります。L2正則化の式は以下のように表されます:
- ここで、λ は正則化率を制御するハイパーパラメータであり、w は重みの値です。
- Regularization rate(正則化率)
- 正則化率は、正則化の強度を制御するためのハイパーパラメータです。正則化率が大きいほど、モデルの複雑さに対するペナルティが増えます。正則化率の値を調整することによって、適切な正則化のバランスを見つけることが重要です。モデルが過学習している場合は、正則化率を増やすことで、汎化性能を向上させることができます。
- ここでは 0 ~ 10 までの 10 分割のうちから設定できます。

- Problem type
- ニューラルネットワークで解こうと思っている問題が分類なのか回帰なのかを指定します。
- ここでは Classification(分類)か Regression(回帰)を選択できます。

- Epoch(エポック)
- DATA
- Which dataset do you want to use?
- データがどのように分布しているかを選択できます。
- Problem type で Classification を選択している場合、Circle、Exclusive、Gaussian、Spiral のうちから、Regression を選択している場合、Plane、Multi Gaussian から選択できます。


- Ratio of training to test data: 10% ~ 90%
- トレーニングデータとテストデータの比率を設定できます。
- ここでは 10% ~ 90% の間で 10% 刻みで設定できます。


- Noise: 0 ~ 50
- ノイズは、データに不要な情報やエラーが混入していることを指します。ニューラルネットワークのコンテキストでは、ノイズは通常、入力データや重みに対する不要な変動やエラーのことを指します。ノイズが存在すると、ネットワークの学習や予測性能に悪影響を与える可能性があります。
- ここでは 0 ~ 50 の間で 5 刻みで設定できます。


- Batch size: 1 ~ 30
- バッチサイズは、ニューラルネットワークの学習中に使用されるサンプルのグループ(バッチ)のサイズを指します。通常、データセットは非常に大きいため、すべてのデータを一度にネットワークに与えることは効率的ではありません。そのため、データセットをバッチに分割し、バッチごとに逐次的に学習を行います。バッチサイズの選択はトレードオフであり、大きなバッチサイズはメモリ使用量を増やす一方、小さなバッチサイズは更新の不安定性を引き起こす可能性があります。一般的に、適切なバッチサイズを選ぶことで、学習の効率性とモデルのパフォーマンスを両立させることができます。
- ここでは 1 ~ 30 の間で 1 刻みで設定できます。
- REGENERATE
- ここをクリックすることでデータを再度分布しなおすことができます。OUTPUT の画像を見ると、REGENERATE をクリックする度に分布がわずかに変わっていくのが分かります。
- Which dataset do you want to use?
- FEATURES
- Which properties do you want to feed in?
- ニューラルネットワークに入力する特徴量を選択できます。
- HIDDEN LAYER
- 隠れ層(中間層)です。層を何層にするか、ニューロンをいくつにするか設定できます。ニューラルネットワークにおいて中間層の増減や各層のニューロン数の変更は、モデルの表現力や学習能力に重要な影響を与えます。
- 隠れ層の増減
- 隠れ層の増加: 隠れ層を増やすことは、ネットワークの表現力を向上させる効果があります。より深いネットワークは、より複雑な特徴を学習できる可能性があります。特に大規模なデータセットや複雑な問題では、より多くの隠れ層を持つネットワークが適切な表現能力を提供することがあります。ただし、過剰な層の追加は過学習のリスクを増やすことに注意が必要です。
- 隠れ層の減少: 隠れ層を減らすと、ネットワークの表現能力が制約される可能性があります。より浅いネットワークでは、複雑なパターンや特徴を学習する能力が制限されることがあります。しかし、簡単な問題や小規模なデータセットの場合は、より浅いネットワークでも十分な表現能力を持つことがあります。
- 各層のニューロン数の増減:
- ニューロン数の増加: 各層のニューロン数を増やすと、ネットワークの表現能力が向上します。より多くのニューロンは、より多くの情報を扱う能力を持ちます。大規模なデータセットや複雑な問題では、より多くのニューロンを持つネットワークが適切な表現能力を提供することがあります。ただし、過剰なニューロン数は計算コストを増加させるだけでなく、過学習のリスクも高めることに注意が必要です。
- ニューロン数の減少: 各層のニューロン数を減らすと、ネットワークの表現能力が制約される可能性があります。より少ないニューロンは、より少ない情報を扱う能力を持ちます。簡単な問題や小規模なデータセットの場合は、より少ないニューロンでも十分な表現能力を持つことがありますが、複雑な問題に対しては表現力が不足する可能性があります。
- ここでは隠れ層の数を最大 6 層、各層のニューロンの数を最大 8 個に設定できます。

- OUTPUT
- 出力層になります。ドットが学習データを表しており、背景色はエリアに対する予測になります。
- Show test data にチェックを入れることで、学習データだけでなくテストデータも表示することができます。

- Discretize output にチェックを入れることで、予測結果を離散化して表示します。

- 色について
- オレンジと青はビジュアライゼーション全体で若干異なる方法で使用されますが、一般にオレンジは負の値を示し、青は正の値を示します。
- データ ポイント (小さな円で表されます) は、最初はオレンジまたは青に色付けされており、正の値と負の値に対応します。
- 隠れ層では、線はニューロン間の接続の重みによって色付けされます。青は正の重みを示します。これは、ネットワークがニューロンの出力を指定どおりに使用していることを意味します。オレンジ色の線は、ネットワークに負の重みが割り当てられていることを示します。
- 出力層では、ドットは元の値に応じてオレンジ色または青色に色付けされます。背景色は、ネットワークが特定のエリアに対して何を予測しているかを示します。色の濃さは、その予測がどの程度信頼できるかを示します。
実際に使用してみる
今回は分類問題に対して使ってみようと思います。まず基本的な Circle の分類を行ってみます。
デフォルトの設定のまま実行すればそこそこ正しく分類してくれます。
Circle 以外のデータ分布の場合でも、概ね入力を変えたりするだけで正しく分類できることが分かります。


最後にうずまき上にデータが分布している場合の分類を行ってみます。
まずデフォルトのまま実行してみます。
エポック数見ればわかりますが、収束するまでかなりかかっているうえに、全然正しく分類できていません。
入力と、ニューロンの数を変えてみました。最初に比べればマシではないでしょうか。。。
ニューラルネットワークは理論上どのような関数の形にも近似することが可能なので、ニューロンや層を増やしたり、パラメータを変更することで、より正確に分類することができるようになります。
また少ないエポックで結果が収束できるように工夫すれば、計算負荷を下げることにもつながります
まとめ
今回はニューラルネットワークの動作を視覚的に学習できる TensorFlow Playground を使ってみました。簡単な設定変更しかしませんでしたが、色々使いながら各パラメータの増減でどのように結果が変わっていくのかを確認するのも勉強になると思います。
気になった方がいればぜひ使ってみてください。