目次
こんにちは。yosshiです。
自身の過去の体験談を元に、統計学でつまずきやすいポイントを分かりやすさ重視で解説するシリーズ、第二弾です。 (前回の内容はこちら)
今回は、中々意味を覚えられない統計用語ランキング一位 (個人調べ) の標準化と正規化について解説をしていきます。
データの前処理に関わる重要な内容なので、是非最後まで見てみて下さい!
※レベルとしては統計検定3級程度の内容を扱います


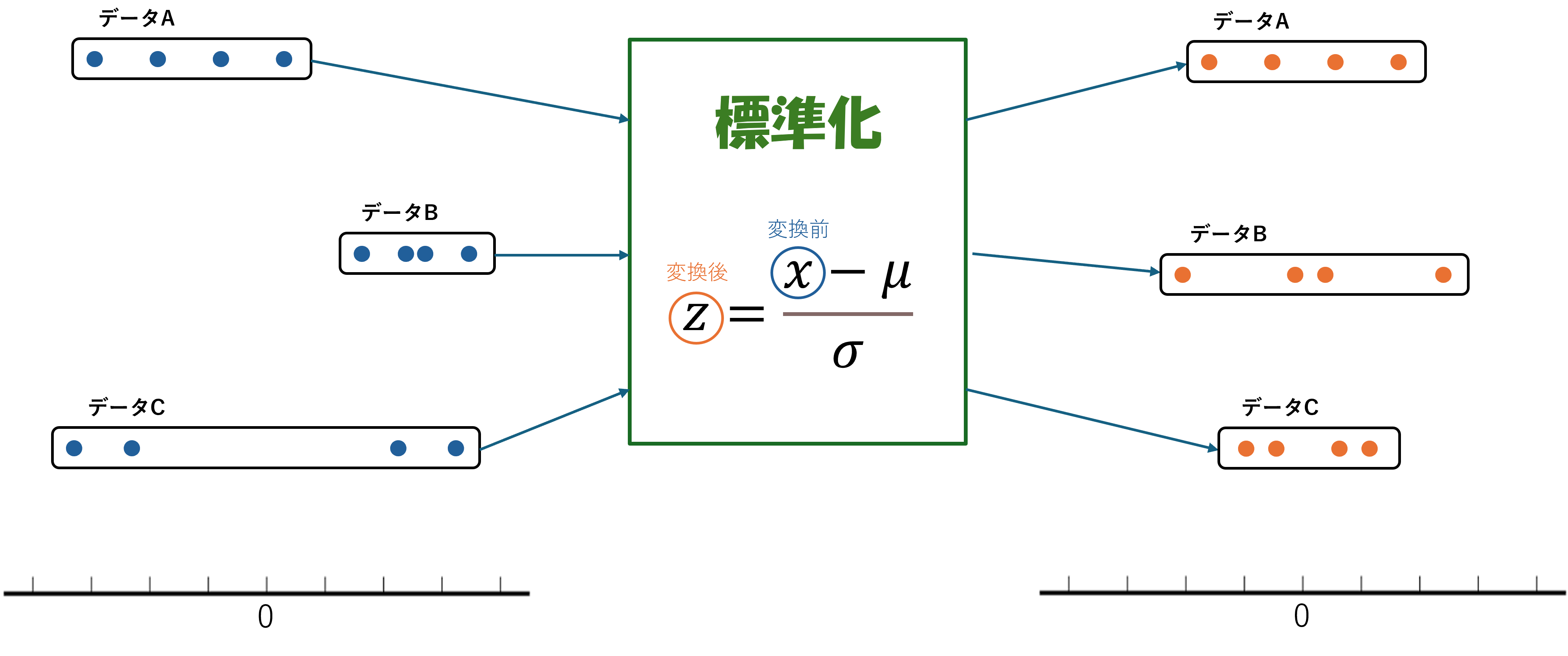
標準化とは、どんなデータでも平均が0, 分散が1のデータに揃えてくれる変換

この変換をするだけで、データの平均とばらつき具合(分散)を均一に揃えることができます。
この変換は「データ(x)から平均(μ)を引き、標準偏差(σ)で割る」という計算をしています。

これで平均値が0のデータに変換されます。

これでばらつき具合が一定(標準偏差が1)のデータに変換されます。
正規化とは、どんなデータでも最小値が0, 最大値が1のデータに揃えてくれる変換

この変換をするだけで、データの範囲を均一に揃えることができます。
この変換は「データ(x)からデータの最小値(xmin)を引き、データの範囲(xmax - xmin)で割る」という計算をしています。

これで最小値が0のデータに変換されます。

これで最大値が1のデータに変換されます。
標準化も正規化も、基本的には異なるデータのスケールを揃えたいときに使用します。
例えば学校が違うA君とB君のテストの点数を比較したい時、そのまま点数を比較してもテストの"平均値"や"分散"、"何点満点か"が違えば「どちらが凄いか」は判断できません。
こういう時は点数をそれぞれ標準化, 正規化をしてスケールを揃えてあげることで、同じ基準で点数を比較することができます。
一方、標準化と正規化にはそれぞれメリットとデメリットがあります。
そのため、データの中身や今後のデータの使い道(分析手法など)を考えて、どちらを使うか決定します。
先ほどの例でピンと来た方もいるかもしれませんが、実は偏差値の計算には今回のテーマの一つである標準化が使われています。
偏差値 = 50 + 10x({得点} - {平均値})/{標準偏差}
点数を標準化して10倍したものに50を足すと偏差値になります。
これにより「別の高校どうし」「別の教科どうし」「別のテストどうし」などを比較することができるというわけです。
また標準化の部分を改めて見てみると、点数が平均値を超えてたら50より高くなることは勿論、データの標準偏差(ばらつき)が少ないほど偏差値が高くなりやすいことも分かります。
殆どの人が50~60点のテストで一人だけ90点を取れた人は相当すごいので、納得感はちゃんとありますね。
余談ですが、ぱっと見で分からない数式が出てきたとき、簡単なデータを入れてみてどういう計算をしているのかの流れを追うことで理解が深まることは結構あります。
今まで意味や公式を丸暗記してしまってた人はぜひ試してみてください。
最後までお読みくださり、ありがとうございました!